L’objectif de ce TP est d’utiliser les formules de modélisation cinématique directe sur un bras à 6 degrés de liberté en simulateur.

Ressources

Lisez les instructions ci-dessous
Objectif
Tout d’abord, installez les dépendances:
pip install numpy pygame pybullet onshape-to-robot transforms3d scipy
Et lancez:
python sim.py
Déplacez les curseurs dans le panneau latéral de droite pour observer le déplacement des 6 degrés de libertés du bras robotique.
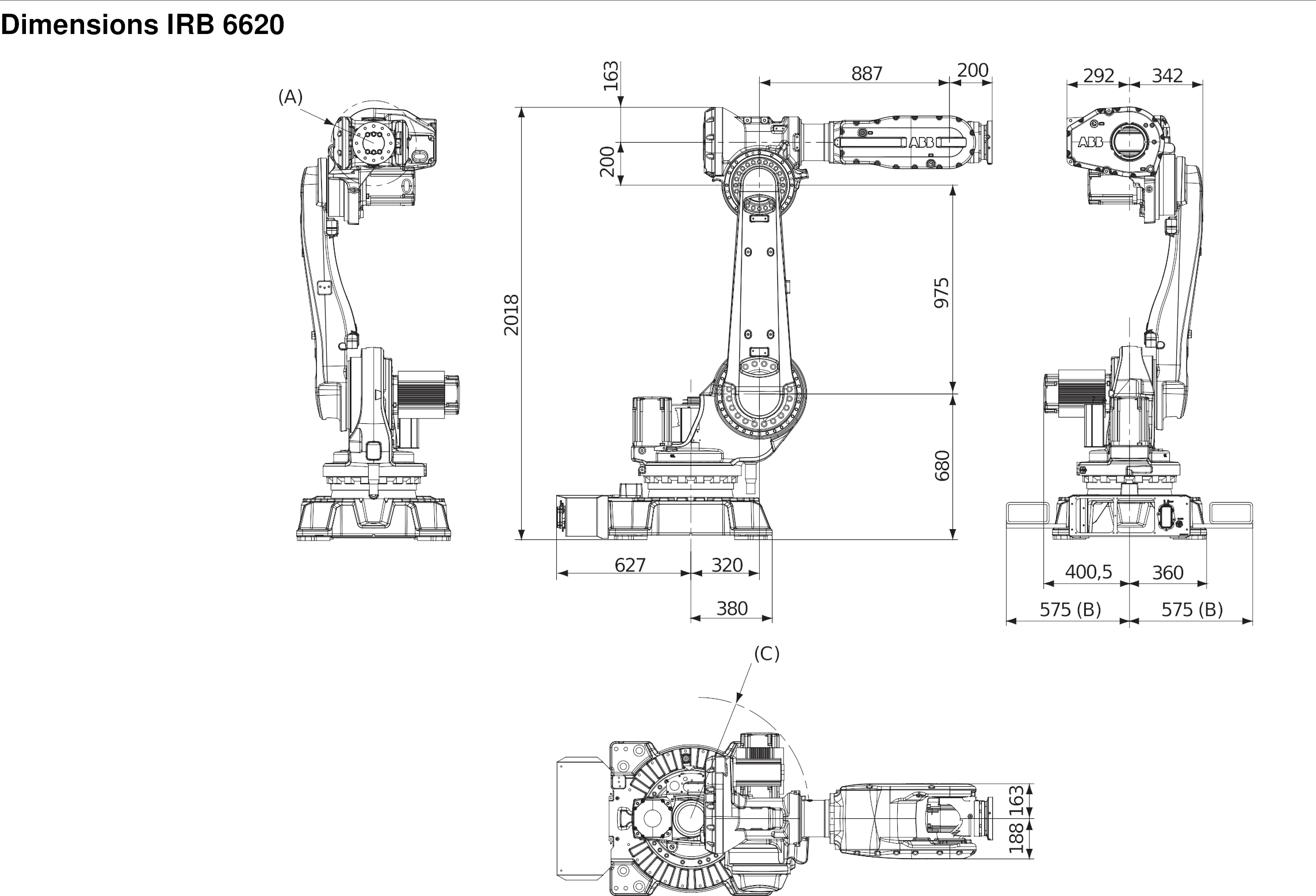
Dimensions
Les dimensions du bras sont indiquées ici, ou dans le fichier drawing.png de l’archive:
Partie 1
1. Modèle géométrique direct
Le but de cette partie est d’implémenter le calcul du modèle géométrique direct du robot, en utilisant les coordonnées homogènes.
Autrement dit, on produira la matrice \(T_{wr}\) permettant de passer du repère de l’effecteur à l’origine du robot, qui est ici l’origine du monde dans le simulateur. Pour rappel, un repère est habituellement dessiné à l’aide de segments rouge, vert et bleu qui représentent respectivement les axes x, y, et z (mémotechnique: “RGB = XYZ”). Dans pyBullet, on remarque d’ailleurs que le repère du monde est dessiné de cette façon à l’origine.
Le repère de l’effecteur est attaché à la dernière pièce du bras 6 axes,sur la surface de la pièce cylindrique surmontée d’une flèche (qui sert ici de repère visuel).
- Récupérez le code python permettant de calculer les transformations 3D homogènes élémentaires (rotations autour des trois axes et translations)
- Exécutez maintenant le code de cette façon:
python sim.py -m direct, constatez qu’un nouveau repère est apparu. Il s’agit du repère obtenu par la matrice de transformation donnée par la fonctiondirectdemodel.py - Implémentez maintenant la fonction
directde manière à retourner la matrice de transformation permettant de passer du repère de l’effecteur à l’origine du robot. - En bougeant les curseurs, valider que cela fonctionne en visualisant le repère qui devrait se positionner systématiquement au bout de l’effecteur.
2. Ajout d’un outil
On souhaite ajouter un outil au bout de l’effecteur. Voici le modèle de l’outil et comment il sera fixé au bout de l’effecteur:
- Déterminez \(T_{et}\), la matrice de transformation permettant de changer de repère de l’outil à l’effecteur du robot
- Implémentez la fonction
direct_toolde manière à ce qu’elle retourneT_world_tool, la matrice qui permet de passer de l’outil au monde (en vous aidant dedirectécrit précédemment)
3. Dessin d’un cercle sur un “tableau”
On propose maintenant de déplacer l’outil de manière à dessiner un cercle sur un “tableau”:

Le tableau sera simplement simulé par un son coin inférieur gauche dans le mode python sim.py -m board.
- Modifier la fonction
boardde manière à ce que l’outil soit plaqué contre le tableau et perpendiculaire à lui. Indication: vous pouvez construire une matriceT_board_toolet l’utiliser. - Modifiez la fonction
boardde manière à ce qu’elle trace un cercle sur le tableau, centré en \([0.2, 0.2]\) et de rayon \(10cm\).
Partie 2
1. Un laser au sol
En exécutant le programme de cette façon: python sim.py -m laser, vous devriez voir un
marqueur au sol apparaître. Ce dernier est le résultat de l’appel à laser(angles) dans
model.py .
Implémentez la méthode laser qui calcule la position du laser au sol en fonction de la
position des moteurs.
2. Modèle géométrique inverse itératif
Dans cette partie, nous allons contrôler le bras robotique à l’aide d’une cible en position et en orientation.
Pour cela, exécutez le code avec python sim.py -m inverse, vous devriez voir apparaître
des curseurs pour contrôler une cible en position et orientation.
- Complétez la fonction
inverseTargetafin qu’elle retourne la matrice complète, en appliquant le roulis, le tangage puis le lacet.
Nous avons ainsi une matrice de transformation \(M\) qui est une cible. Si on note \(\alpha\) le vecteur des angles \(\alpha_i\) des moteurs, notre objectif est de trouver le vecteur \(\alpha\) tel que le modèle direct du bras aie pour matrice \(M\). Autrement dit, \(M = D(\alpha)\). Le problème est que l’inversion de \(D\) n’est pas un problème facile (voire possible) dans le cas général, nous allons donc utiliser une méthode itérative.
L’idée de cette méthode est de calculer un score, qui est d’autant plus petit que notre estimation est bonne. Pour ce faire, nous allons attacher 4 points au repère cible, que nous nommerons \(P_1\), \(P_2\), \(P_3\) et \(P_4\), qui sont respectivement la position des points \((0,0,0)\), \((0.1,0,0)\), \((0,0.1,0)\) et \((0,0,0.1)\) dans le repère cible.
Pour un candidat \(\hat \alpha\), on calculera d’abord \(D(\hat \alpha)\), et ensuite la position de ces 4 même points, on pourra alors mesurer la distance entre ces points et les points cibles:
(Note: cette méthode fonctionne, mais ça n’est pas la bonne façon de prendre en compte une erreur en orientation 3D)
La somme de ces distances est une erreur que l’on souhaite minimiser. On utilisera la méthode
scipy.minimize pour minimiser notre fonction.
- Implémentez la méthode
points, qui prend en paramètre une matrice de transformation homogène et retourne la position des 4 points expliqués ci-dessus dans le repère. - Implémentez la méthode
inverse, qui prend en paramètre la position actuelle des angles ainsi que la position et l’orientation cible donnés par les sliders. L’objectif de cette méthode est de trouver des angles permettant d’atteindre cette position et cette orientation en s’appuyant sur la fonction de score expliquée ci-dessus et surscipy.minimizepour trouver le meilleur candidat.
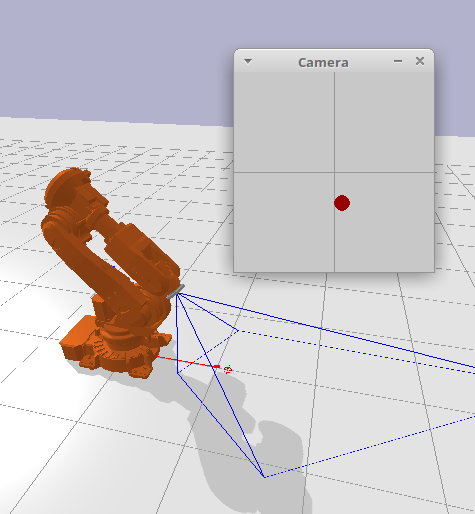
3. Une caméra
Supposons qu’une caméra soit accrochée au bout du bras du robot. On souhaite savoir comment un point \(P\) se projette dans l’image de la caméra. Pour ce faire, on calcule tout d’abord la position du point dans le repère de la caméra (cf figure ci-dessous), que l’on nomme \(x_P, y_P, z_P\).
Ensuite, on projette ce point dans le plan \(J\), définit par une distance focale \(f\) au centre optique de la caméra \(C\). Notre écran étant virtuel, le nombre de pixels par mètre peut être défini arbitrairement (par exemple \(1\)). (Ce modèle classique se nomme Pinhole camera model).
La caméra que nous allons simuler ici produit une image carrée de \(w \times w\) pixels, et elle sera caractérisée par son angle d’ouverture \(\alpha\).
- Exprimez la distance focale \(f\) en fonction de \(w\) et \(\alpha\)
- À partir de la position d’un point connue dans le repère du monde, comment connaître la position de ce point dans le repère de l’effecteur (et donc ici de la caméra)?
- Comment calculer la taille (en pixels) d’une sphère de rayon connu \(r\) (mètres) dans l’image?
- Implémentez la fonction
cameradansmodel.py. Cette fonction reçoit en paramètre les angles du bras robotique, la position de la cible que vous pouvez déplacer en 3D à l’aide des curseurs, la taille de l’image en pixels, et l’angle d’ouverture de la caméra (également changeable à l’aide des curseurs). La fonction retourne la position de la balle dans l’image (\(0,0\) étant le centre de l’image) ainsi que sa taille (un rayon en pixels). La cible a un rayon de \(42mm\).- En lançant le programme avec
python sim.py -m camera, la fonction sera appelée et le résultat sera dessiné dans une autre fenêtre
- En lançant le programme avec
- Implémentez la fonction
camera2, qui retourne la position des coins de l’image qui serait sur un écran situé à 2m, sauf si ce faisceau intersecte le sol.- Pour tester, lancez le programme avec
python sim.py -m camera2. Le résultat final doit ressembler à la figure ci-dessous.
- Pour tester, lancez le programme avec
 Rhoban
Rhoban
 @RhobanRobots
@RhobanRobots