Jusqu’ici, nous avons abordé le concept de repères et de changement de repères en 2D. Dans cette partie, nous allons transposer ce que nous avons vu au cas de la 3D.
Repère 3D
Un repère 3D est équipé d’un troisième vecteur dans sa base, par exemple \((O, \vec{i}, \vec{j}, \vec{k})\):
En respectant les contraintes d’un repère orthonormé (vecteurs unitaires et orthogonaux deux à deux), et une fois que l’on choisit \(\vec{i}\) et \(\vec{j}\), il reste deux choix pour \(\vec{k}\). Le choix que l’on fera sera toujours celui de la figure ci-dessus: c’est ce qu’on appelle un repère direct.
Rotations 3D
Une matrice de rotation 3D est une matrice qui permet de changer de base d’un repère 3D orthonormé vers un autre.
\[R = \begin{bmatrix} r_{11} & r_{11} & r_{11} \\ r_{21} & r_{21} & r_{21} \\ r_{31} & r_{31} & r_{31} \end{bmatrix}\]Si on multiplie la matrice par le vecteur \(\begin{bmatrix}1 \\ 0 \\ 0\end{bmatrix}\), on obtiendra les coordonnées du premier vecteur de la base de départ exprimées dans la base d’arrivées. Or, ces coordonnées sont exactement la première colonne de la matrice.
Si une matrice \(R_{r_1 r_2}\) permet de passer d’un repère \(\{ r_2 \} = (O, \vec{i'}, \vec{j'}, \vec{k'})\) à un repère \(\{ r_1 \} = (O, \vec{i}, \vec{j}, \vec{k})\), alors les colonnes de cette matrice sont les coordonnées des vecteurs \(\vec{i'}, \vec{j'}, \vec{k'}\) exprimés dans \(\{ r_1 \}\):
\[R_{r_1 r_2} = \begin{bmatrix} \vec{i'}_{r_1} & \vec{j'}_{r_1} & \vec{k'}_{r_1} \end{bmatrix}\]Ainsi, une matrice de rotation 3D est composée de 9 nombres, mais de 6 contraintes, car 3 nombres suffisent pour représenter une orientation 3D:
- Les colonnes sont orthogonales deux à deux (3 contraintes)
- Les colonnes sont de longueur unitaire (3 contraintes).
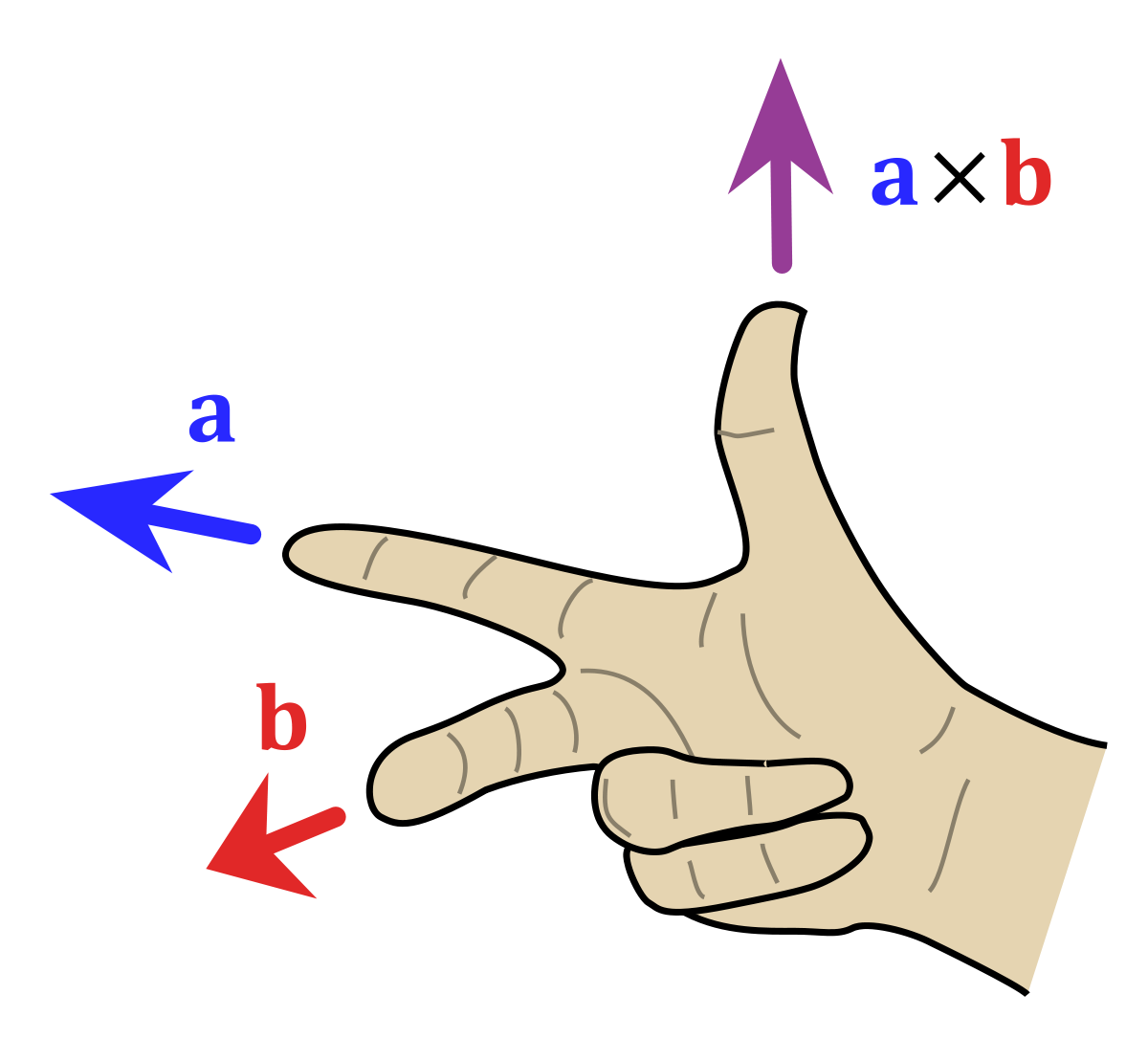
- Le produit vectoriel de la première colonne par la deuxième est égal à la troisième colonne
Cette troisième contrainte est en fait ici pour imposer une convention afin que le repère soit direct. Intuitivement, si on fixait deux vecteurs \(x\) et \(y\) unitaires et orthogonaux, elle permet d’imposer la direction du vecteur \(z\). Une manière de se rapeller de cette direction est d’utiliser la règle de la main droite:
Rotations 3D élémentaires
En 3D, on peut tout d’abord représenter les trois rotations élémentaires, autour des axes \(x\), \(y\) et \(z\). Par convention, voici le sens de ces rotations:
Pour se souvenir de cette convention, voici un mémotechnique:
Un autre mémotechnique est de regarder dans quel sens s’enroule la main droite autour du pouce lorsqu’il est aligné avec l’axe autour duquel on veut tourner.
En se plaçant dans les plans correspondant, on peut donc en déduire les matrices de rotation 3D suivantes:
\[R_x(\alpha) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & cos(\alpha) & -sin(\alpha) \\ 0 & sin(\alpha) & cos(\alpha) \end{bmatrix}\] \[R_y(\alpha) = \begin{bmatrix} cos(\alpha) & 0 & sin(\alpha) \\ 0 & 1 & 0 \\ -sin(\alpha) & 0 & cos(\alpha) \end{bmatrix}\] \[R_z(\alpha) = \begin{bmatrix} cos(\alpha) & -sin(\alpha) & 0 \\ sin(\alpha) & cos(\alpha) & 0 \\ 0 & 0 & 1 \end{bmatrix}\]Propriétés
Composition
On peut composer des rotations 3D en multipliant les matrices successivement. Par exemple, toute rotation 3D peut être obtenue par multiplication successives des trois rotations élémentaires:
\[R = R_x(\phi) R_y(\theta) R_z(\psi)\]On peut représenter une orientation 3D par ces trois angles \((\phi, \theta, \psi)\), c’est ce qu’on appelle les angles d’Euler. Dans ce cas, les noms tangage, roulis et lacet (en anglais pitch, roll et yaw) sont utilisé pour désigner les angles respectivement autour de l’axe \(x\), \(y\) et \(z\):
Inversion
De la même manière qu’en 2D, la transposée d’une matrice de rotation est également son inverse:
\[R^T = R^{-1} \space \space \space \space (1)\]Coordonnées homogènes 3D
Présentation
On peut également utiliser les coordonnées homogènes en 3D, les matrices de transformations ressembleront alors à:
\[T_{a b} = \begin{bmatrix} R_{a b} & t_{a b} \\ 0_{1 \times 3} & 1 \end{bmatrix}\]Où:
- \(R_{a b}\) est la matrice de changement de base de \(b\) vers \(a\),
- \(t_{a b}\) est la coordonnée (vecteur de taille 3) de l’origine du repère \(\{ b \}\) exprimée dans \(\{ a \}\)
Inversion
Grâce à l’équation \((1)\), la même formule d’inversion fonctionne:
\[T_{b a} = T_{a b}^{-1} = \begin{bmatrix} R_{a b}^{-1} & -R_{a b}^{-1} t_{a b} \\ 0_{1 \times 3} & 1 \end{bmatrix}\]Dans la prochaine partie, nous verrons comment cela peut s’appliquer à la modélisation d’un robot articulaire
 Rhoban
Rhoban
 @RhobanRobots
@RhobanRobots