Bras 3 axes

« Retour au sommaire

L’objectif de ce TP est d’utiliser les formules de modélisation cinématique directe sur un bras à 6 degrés de liberté en simulateur.

Ressources

Téléchargez l'archive tp_3axis.zip
Lisez les instructions ci-dessous

Objectif

Tout d’abord, installez les dépendances:

pip install numpy pygame pybullet onshape-to-robot transforms3d scipy

Et lancez:

python sim.py

Déplacez les curseurs dans le panneau latéral de droite pour observer le déplacement des 6 degrés de libertés du bras robotique.

Dimensions

Les dimensions du bras sont indiquées ici, ou dans le fichier drawing.pdf de l’archive.

1. Modèle géométrique direct

Exécutez le programme avec python sim.py -m direct, vous devriez voir apparaître trois curseurs qui permettent de contrôler les trois moteurs du robots, ainsi qu’une cible immobile:

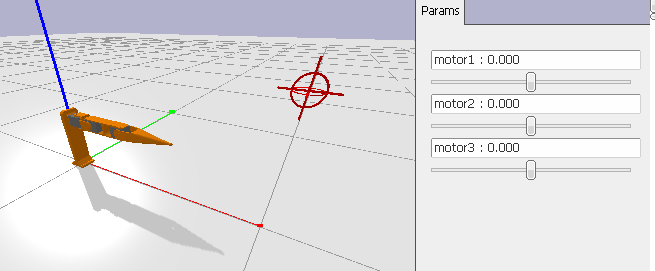
Implémentez la méthode direct dans model.py, qui prend en paramètre la position des moteurs (radians) du robot et retourne la position du bout de l’effecteur.

2. Modèle géométrique inverse analytique

Exécutez le programme avec python sim.py -m inverse. Cette fois, vous pouvez piloter la position cible à l’aide des curseurs.

Implémentez la méthode inverse dans model.py, qui prend en paramètre la position cible et retourne les trois angles à utiliser pour l’atteindre.

De cette manière, le bout du bras devrait coïncider (lorsque c’est possible) avec la position cible donnée.

3. Modèle géométrique inverse itératif

Au lieu de résoudre analytiquement le modèle géométrique, il existe une autre approche, qui consiste à se baser sur le modèle géométrique direct, et tenter de trouver par essais successifs les $\alpha_i$ qui minimisent une fonction d’erreur.

Si nous notons $D(\alpha)$ le modèle direct (où $\alpha$ est le vecteur des $\alpha_i$), alors le score d’un candidat $\hat \alpha$ peut être la distance entre le bout de l’effecteur obtenu par le modèle direct et ce point $|| D(\hat \alpha)-T ||$.

Ainsi, le but est de trouver le candidat $\hat \alpha$ qui minimise ce score. Cette opération peut s’effectuer en utilisant scipy.minimize.

Implémentez la fonction inverseIterative, qui fais la même chose que inverse, mais sans utiliser la solution géométrique analytique, en utilisant le modèle inverse, une fonction de score et scipy.minimize.

4. Un triangle

Maintenant que nous pouvons contrôler le bout du bras en cartésien ($x$, $y$, $z$), nous allons lui faire suivre une trajectoire en forme de triangle.

Ce triangle sera paramétré par (cf figure ci-dessous):

triangle_x: la position x du triangle,
triangle_z: la hauteur de la base du triangle,
triangle_h: la hauteur du triangle,
triangle_w: la largeur du triangle.

Implémentez la méthode trianglePoints dans model.py, afin qu’elle retourne la position des 3 points du triangle.

Si vous exécutez le programme à l’aide de python sim.py -m triangle-points, vous devriez voir le triangle apparaître. Essayez de bouger les curseurs, le triangle devrait s’adapter.

Implémentez maintenant la méthode triangle de model.py, afin de produire les angles du bras robotique tels que le bout de ce dernier parcours le triangle.

Le paramètre t est ici le temps (en secondes) écoulé depuis le début de la simulation, il peut être utilisé par tranches (par exemple, de $t=0$ à $t=1$, on parcours le premier segment, de $t=1$ à $t=2$ le second etc.).

Testez avec python sim.py -m triangle.

5. Un cercle

Cette fois-ci, nous allons faire parcourir un cercle au bras robotique. Il sera caractérisé par:

circle_x la position $x$ du centre du cercle,
circle_z la position $z$ du centre du cercle,
circle_r le rayon du cercle,
circle_duration la durée de parcours du cercle.
Implémentez la méthode circlePoints dans model.py, qui retourne N points répartis sur un cercle dont les paramètres lui sont fournis.

Lancez le programme avec python sim.py -m circle-points et testez votre code à l’aide des curseurs.

Implémentez la méthode circle, dans laquelle le bras robotique devra suivre la trajectoire du cercle.

Testez votre code avec python sim.py -m circle.