Prise en main du simulateur

---

« Retour

Ici, nous allons prendre en main le simulateur qui sera utilisé au cours de ce TP guidé.

Introduction

Premièrement, lancez:

python simulator.py

Dans le dossier quadruped/ et observez ce qu’il se passe. Vous pouvez si vous le souhaitez regarder le code de simulator.py, mais vous n’aurez pas à le modifier.

Ce script prend en argument un mode de fonctionnement. Par défaut, il vous propose de régler les valeurs cibles des angles moteur en direct avec les paramètres latéraux:

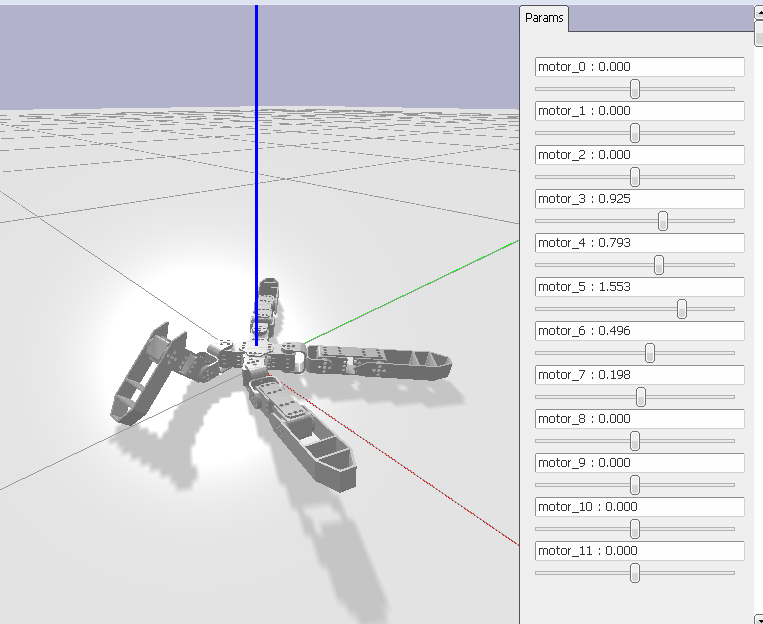
Le mode sandbox

Votre objectif au cours du TP sera d’implémenter les méthodes du fichier control.py. Dans cette séance, nous allons écrire du code permettant de produire des angles cibles pour les moteurs du robot.

Lancez:

python simulator.py -m sandbox

Et regardez le code de la fonction sandbox de control.py. Ce dernier produit des valeurs cibles pour les moteurs qui sont des oscillations sinusoïdales sin(t).

En changeant le code afin qu’il retourne une liste d’angles cibles, vous pourrez produire votre mouvement.

Position immobile

Remarquez qu’en position “0”, le robot est couché par terre.

Dans un premier temps, modifiez la fonction sandbox afin qu’elle positionne le robot dans une posture immobile dans laquelle le robot est “debout”.

Un premier déplacement

En faisant appel à votre imagination, créez un premier mouvement de déplacement.

Vous allez voir rapidement que cela n’est pas immédiat. Pour cette première approche vous pouvez appliquer la stratégie suivante:

• Considérer une succession arbitraire d’intervalles de temps \(I_k\) partitionnant une durée finie qui sera la période \(p\) du mouvement. Période que vous fixerez également de façon arbitraire.
• Pour chacun de ces intervalles \(I_k\), définissez une position \(P_k\) du robot. Cette position est arbitraire, comme la position immobile, c’est à vous de la définir pour créer votre mouvement.

La fonction pourra alors:

• Déterminer l’intervalle \(I_k\) auquel appartient t, ou plus exactement t % p,
• Retourner la position \(P_k\) correspondante.

---

Dans la prochaine partie, nous étudierons le modèle cinématique inverse d’une patte du robot.