L’objectif de ce TP est de résoudre la cinématique directe et inverse d’un simple pan/tilt. Après avoir résolu le problème analytiquement, nous verrons comment approximer ce modèle à l’aide d’un réseau de neuronnes.
Ressources
Lisez les instructions ci-dessous
Objectif
Tout d’abord, installez les dépendances:
pip install numpy pygame pybullet onshape-to-robot transforms3d scipy
Et lancez:
python sim.py
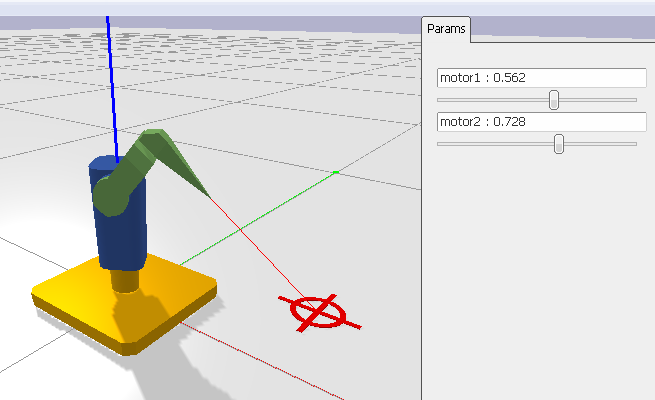
Déplacez les curseurs dans le panneau latéral de droite pour observer le déplacement des 6 degrés de libertés du bras robotique.
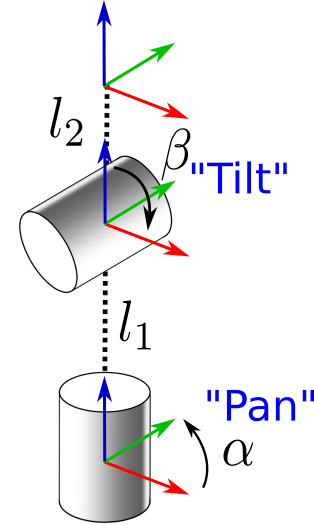
Dimensions
Voici la structure du robot ainsi que les angles des degrés de liberté:
Partie 1
1. Modèle géométrique direct
Dans model.py, implémentez la méthode direct, qui prend en entrée les deux angles du robot, et produit la matrice
de transformation \(T_{we}\) 4x4 allant de l’effecteur au monde.
Pour tester, lancez le programme de cette façon:
python sim.py -m direct
2. Intersection avec le sol
Implémentez maintenant la méthode laser, qui calcule l’intersection au sol d’un laser qui partirait de l’axe \(x\)
de l’effecteur.
Pour tester, lancez le programme de cette façon:
python sim.py -m laser
Voici le résultat que vous devriez obtenir
3. Modèle inverse analytique
Implémentez la méthode inverse, qui calcule les angles cibles afin de regarder un point au sol fourni par l’utilisateur.
Pour tester, lancez le programme de cette façon:
python sim.py -m inverse
4. Modèle inverse appris
Nous allons maintenant apprendre le modèle inverse, à l’aide de réseaux de neurones comme approximateurs de fonction. Pour cela, nous allons suivre la procédure suivante:
- Générer une configuration aléatoire du robot
- Appeler la fonction
laserafin d’obtenir la position au sol - Utiliser ces données pour entraîner un réseau de neuronnes.
Pour cette dernière étape, vous pourrez vous inspirer de learn_example.py.
Pour tester, lancez le programme de cette façon:
python sim.py -m inverse_nn
Rhoban
@RhobanRobots